Why do I always say to take large distances in space, say to galaxies in a Hubble deep field image, with a grain of salt? The main reason is that, in an expanding cosmology, the meaning of distance is not a simple concept.
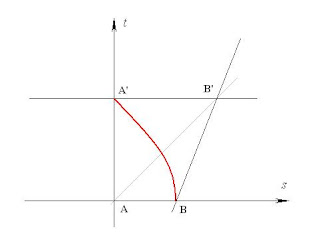
In the diagram we represent space with the horizontal s-axis and time with the vertical t-axis. There are two galaxies and both are stationary in the space around them. However, because space (s) is expanding, B is getting farther from A, not because B or A is moving, but because the space is expanding.
At the point in space and time, B, a photon of light leaves that galaxy and travels to our galaxy where it arrives at A', later in time. The red path represents the path the photon takes through spacetime.
The red path of the photon is curved which is a consequence of the expansion of space as it travels.
How far away?
Now, everyone wants to ask the question (when we at A' look at our picture of B), how far away is B? Well, there are at least three distances here. There's the distance AB, there's the distance A'B' and there's the path the light actually took BA'. When someone says the distance is 13 billion light years, which one of these are they talking about? If your answer is that you don't know, well, I don't know either.
The problem is actually worse than this. In my diagram, I've represented space as expanding at a uniform rate. That rate would be represented by the slope of the BB' line. However, space doesn't really expand at a uniform rate but at a changing rate. Worse, it's lately come to light that the rate is increasing, i.e., the expansion seems to be accelerating. So, the BB' line wouldn't even be a straight line in this diagram. The BA' photon path would be different.
A tale of two numbers
In fact, how you draw this diagram in detail depends on the cosmological model of how space expands with time. You can write it down as a simple function of scale and time, R(t). However, we don't really know well what the current rate d R(t) / dt is, or even the acceleration d2 R(t) / dt2 is. By the way, the rate is called the Hubble constant. (Of course, if there's acceleration, then that speed isn't a constant).
What do we know?
There is really only one thing we know with high accuracy from these observations. The wavelength of light when emitted at B was proportional to the length AB. The wavelength of light received at A' is proportional to the length A'B'. So the ratio of A'B' / AB is equal to the ratio of the wavelengths.
The redshift is expressed as a value called z. If the new wavelength is three times the original length (i.e., the ratio is 3), astronomers say the redshift z = 2. That's because you add two more of those wavelengths to the one you started with to get 3, or you shifted it by the amount 2.
So the one thing we know is that scale of the universe (the distance between distant galaxies that are sitting still) is z + 1 times bigger than when the light was emitted.
That's why I'd rather just hear the redshift for these observations and leave the other details to be figured out some day.
How far have we seen?
Some recent record observations of redshift are around z = 7, so we've seen some objects as they were when the scale of the universe was 1/8 it's current scale.
Of course this is also model-dependent, based on the concepts of cosmological redshift and general relativity!
__________
I think the phrase “a tale of two numbers” should be attributed to Edward R. Harrison, probably from his book Cosmology: The Science of the Universe.